Tugas 6: Mengaplikasikan Geogebra Untuk Materi Geometri Kontekstual

Deskripsi Masalah

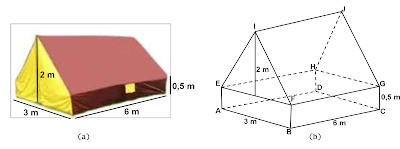
Sebuah tenda berbentuk bangun seperti gambar di bawah ini. Berapakah luas kain yang digunakan untuk membuat sebuah tenda seperti itu, bila alasnya berbentuk persegipanjang dengan panjang 6 m, lebar 3 m dan tingginya 0,5 m. Sedangkan tinggi tenda 2 m.

Alternatif Penyelesaian

Perhatikan ilustrasi gambar berikut:

Berdasarkan ilustrasi gambar di atas, terdapat gabungan dua bentuk bangun ruang yaitu bagian bawah tenda adalah balok dan bagian atas tenda adalah prisma segitiga. Kemudian, untuk mengetahui banyaknya luas kain yang digunakan untuk tenda tersebut berarti kita dapat menggunakan cara dengan menghitung luas permukaan dan volume masing-masing bangun ruang tersebut, yakni sebagai berikut:

(i) Perhatikan gambar balok berikut:

Untuk menentukan luas permukaan balok tersebut kita perhatikan dulu gambar tenda , bahwa luas permukaan kain pada balok tersebut tanpa alas dan tutup, yakni sebagai berikut.

$\text{Luas permukaan balok tanpa alas dan tutup}=2\left(\text{AB}\times \text{AE}+\text{BC}\times \text{CG}\right)$
$=2\left(3\times 0\text{,}5+6\times 0\text{,}5\right)$
$=2\left(1\text{,}5+3\right)$
$=2\left(4\text{,}5\right)$
$=9{\text{ m}}^2$

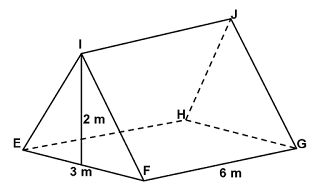
(ii) Perhatikan gambar prisma berikut:

Untuk menentukan luas permukaan prisma tersebut kita perhatikan dulu gambar tenda bagian atas, bahwa luas permukaan kain pada prisma tersebut luas persegi panjang EFGH, yakni sebagai berikut:

$\text{Luas permukaan prisma tanpa luas EFGH}=2\times \text{luas segitiga EFI}+2\times \text{luas FGJI}$
$=2\left(\frac{1}{2}\times 3\times 2\right)+2\times 6\times \text{FI}$

cara mencari panjang FI atau sisi miring dari segitiga EFI adalah sebagai berikut:

$\text{dengan dalil phytagoras di dapat panjang FI}=\sqrt{{\left(1\text{,}5\right)}^2+2^2}=\sqrt{6\text{,}25}=2\text{,}5$

Sehingga,
$\text{Luas permukaan prisma tanpa luas EFGH}=2\times \text{luas segitiga EFI}+2\times \text{luas FGJI}$
$=2\left(\frac{1}{2}\times 3\times 2\right)+2\times 6\times \text{FI}$
$=6+12\times 2\text{,}5$
$=36{\text{ m}}^2$

Jadi, banyaknya kain yang digunakan untuk membuat satu buah tenda tersebut adalah :
Luas permukaan balok tanpa alas dan tutup + Luas permukaan prisma tanpa luas EFGH = $9{\text{ m}}^2+36{\text{ m}}^2=45{\text{ m}}^2$

Tugas 5: Media Pembelajaran Menyisipkan Link Materi Limas Segi-empat

LIMAS SEGI EMPAT

A. Pengertian Limas Segi Empat

Limas adalah suatu bangun ruang yang dibatasi oleh sebuah segi banyak (segi n) dan segitiga-segitiga yang mempunyai titik puncak persekutuan di luar bidang segibanyak itu. Atau dapat juga di artikan limas adalah bangun ruang yang dibatasi oleh sebuah segitiga ataupun segibanyak sebagai alas dan beberapa buah bidang berbentuk segitiga sebagai bidang tegak yang bertemu pada satu titik puncak. limas diberi nama berdasarkan bentuk segi - pada bidang alas.

Seperti prisma, nama limas juga berdasarkan jumlah segi-n sisi alasnya. Apabila alas limas berupa segi-n beraturan dan tiap sisi tegak merupakan segitiga sama kaki yang beraturan, maka limasnya disebut limas segi-n beraturan. Di sini kita akan membahas limas segi-empat beraturan. Limas segi empat beraturan adalah limas yang memiliki alas berbentuk segi empat yang beraturan, misalnya alasnya berbentuk persegi, persegi panjang, layang-layang, dan belah ketupat.

B. Unsur-unsur limas Segi Empat

Unsur-unsur yang dimiliki limas dengan alas segi-empat, yaitu :
1.Titik sudut
2.Rusuk limas
3.Bidang sisi
4.Bidang alas
5.Bidang sisi tegak
6.Titik puncak
7.Tinggi limas
8.Diagonal bidang /sisi
9.Diagonal ruang

C. Jaring-jaring Limas Segi Empat

Limas apabila diiris sepanjang rusuk-rusuknya kemudian dibentangkan sehingga membentuk bidang datar, maka disebut jaring-jaring limas. Di bawah ini adalah gambar jaring-jaring limas segi-empat:

D. Volume Limas Segi Empat

$6\times \text{Volume Limas}=\text{Volume Kubus}$

$\text{Volume Limas}=\frac{1}{6}\times \text{Volume Kubus}$

$=\frac{1}{6}\times \text{s}\times \text{s}\times \text{s}$

$=\frac{1}{6}\times \left(\text{s}\times \text{s}\right)\times 2\times \frac{1}{2}\text{s}$

$=\frac{1}{6}\times 2\times \text{luas bidang alas}\times \text{Tinggi Limas}$

$=\frac{1}{3}\times \text{Luas alas}\times \text{Tinggi Limas}$

Jadi, didapatkan rumus untuk menghitung volume limas adalah sebagai berikut:

$$\text{Volume Limas}=\frac{1}{3}\times \text{Luas alas}\times \text{Tinggi Limas}$$

Setelah kita telah membahas tentang volume limas. Mari kita belajar untuk membuat limas segi-empat beraturan dengan menggunakan aplikasi geogebra.
Tutorial Membuat Limas Segi-empat Beraturan Dengan Menggunakan Geogebra

Tugas 5: Tutorial membuat limas segi-empat beraturan dengan menggunakan geogebra

TUTORIAL MEMBUAT LIMAS SEGI-EMPAT BERATURAN DENGAN MENGGUNAKAN GEOGEBRA

Buka aplikasi geogebra
Pilih toolbar dengan simbol poligon dan pilih icon poligon, seperti gambar di bawah ini

Buatlah empat titik sudut yang akan dijadikan bidang alas dari limas segi-empat dengan ukuran sesuai dari keinginan masing-masing.

Setelah alas segiempat sudah dibentuk. Pilih menu-bar view lalu klik 3-D Graphic untuk menampilkan 3 Dimensi, karena jika kita menggambar bangun ruang maka kita berbicara di bidang 3 dimensi di Koordinat Cartesius

Setelah kita mengklik 3D Graphic maka tampilan yang akan muncul adalah seperti gambar di bawah ini:

Kemudian klik alas limas pada tampilan 3 dimensi, lalu pilih toolbar dengan gambar pyramid, lalu pilih extrude to pyramid or cone untuk membuat tinggi limas.

Setelah sudah mengklik pilihan extrude to pyramid or cone , maka akan muncul kotak dialog Altitude secara otomatis, kemudian masukkan ukuran tinggi limas sesuai keinginan kita

Misalnya kita ingin tinggi limas dengan ukuran 5 satuan. Lalu klik OK.

Setelah kita klik OK, maka akan muncul hasilnya, yaitu bangun limas segi empat beraturan di tampilan 3 Dimensi.

Kemudian kita harus membuat tinggi limas dengan cara, membuat titik potong dari diagonal sisi alas limas dengan cara membuat segment diagonal dari sisi alas terlebih dahulu seperti gambar di bawah ini :





Kemudian pilih perintah intersect untuk menemukan titik potong 2 diagonal sisi tersebut


Lalu Hubungkan titik potong diagonal alas tersebut dengan titik puncak limas melalui perintah segment

Maka kita telah selesai membuat limas segi empat beraturan